Symétrie axiale
Ce modèle numérique convient à l'analyse des structures de révolution (c'est-à-dire présentant un axe de symétrie). Cette hypothèse doit être satisfaite à la fois du point de vue de la structure et de la charge. Un exemple typique est l'étude de pieu isolé chargé verticalement, l'excavation d'un fossé circulaire ou le pompage d'eau à partir d'un trou circulaire.
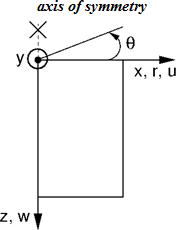 Analyse axisymétrique
Analyse axisymétrique
Comme pour l'analyse en déformation plane, le problème de calcul est tridimensionnel, mais peut être ramené à un problème bidimensionnel, cf. figure. L'analyse est ensuite réalisée sur 1 m de longueur d'arc de diamètre x(r). L'axe de symétrie correspond toujours à l'origine de la coordonnée x(r). Les composantes de la contrainte de cisaillement dans le sens de la rotation peuvent être négligées. On se retrouve alors avec les composantes de contrainte et de déformation agissant sur le plan de coupe symétrique et les composantes de déformation normale et de contrainte dans la direction tangentielle (direction circonférentielle). Les composantes non nulles correspondantes des vecteurs de contrainte et de déformation sont :
![]()
![]()
Il est clair que la déformation tangentielle, et donc aussi les contraintes normales, atteignent une valeur infinie au niveau de l’axe de symétrie. Ainsi, en ce qui concerne l'approximation par éléments finis, l'obtention d'estimations fiables et suffisamment précises de ces valeurs nécessite un maillage relativement fin le long de l'axe de symétrie.
L’application de charges linéiques et surfaciques mérite également d’être mentionnée. Plusieurs exemples d'application de la charge sur une surface de terrain sont présentés dans la figure suivante. Clairement, leur effet augmente avec la distance par rapport à l'axe de symétrie. L'introduction d'un tel type de charge directement sur l'axe de symétrie n'a donc aucun effet. Dans un tel cas, il est nécessaire de choisir le type de charge d'axe de symétrie. Le programme ne permet que l'application de forces concentrées.
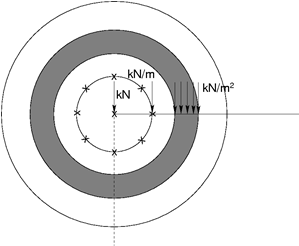 Exemples de charge appliquée sur une surface de terrain
Exemples de charge appliquée sur une surface de terrain
Concernant les éléments de poutre, l’analyse correspond à la solution d’une membrane plane de révolution comportant des effets de flexion. Les degrés de liberté non nuls sont identiques à ceux adoptés pour les éléments de poutre dans l'analyse en déformation plane. Outre les effets axiaux (méridiens), il est nécessaire de prendre également en compte les effets de membrane et de flexion dans la direction tangentielle, comme l'illustre la figure suivante.
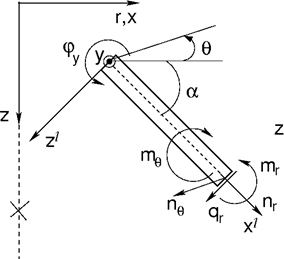 Elément de poutre en symétrie axiale
Elément de poutre en symétrie axiale
Les composantes des efforts internes correspondantes (cf. figure), pour 1 m de largeur de section, sont données par :
![]()
Dans le cas particulier d'une plaque circulaire (angle α = 0), la figure suivante montre que l'on peut se référer aux composantes radiales et tangentielles des efforts internes.
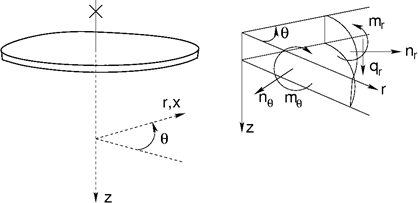 Efforts internes agissant sur une plaque circulaire
Efforts internes agissant sur une plaque circulaire
Les forces internes sont liées aux déformations et aux courbures correspondantes comme suit:
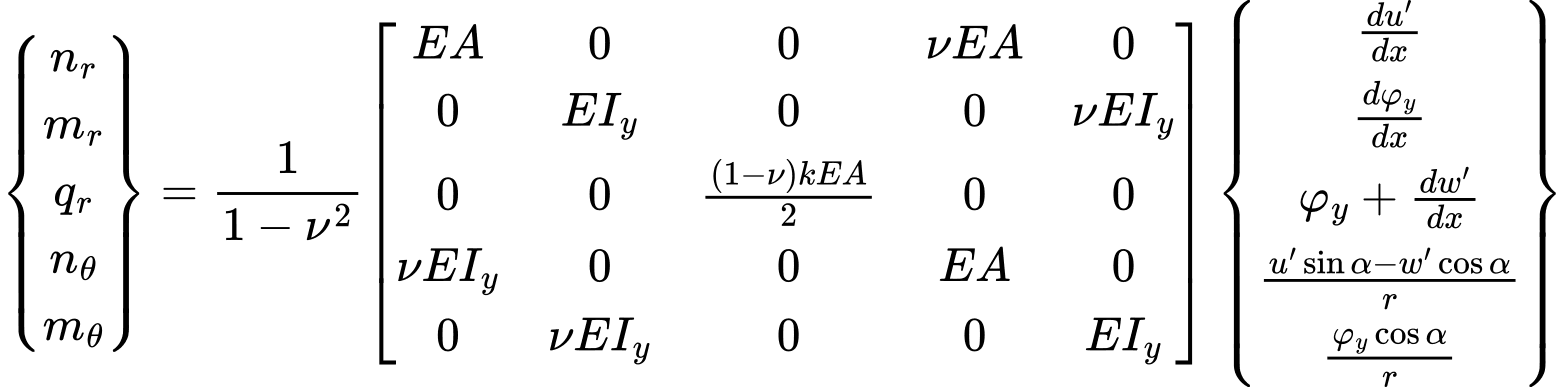
Lorsque r tend vers l'infini, on arrive aux conditions de déformation plane. Il convient de noter qu'en cas de forces de cisaillement, leurs intensités dépendent, contrairement à l'analyse en déformation plane, du raffinement du maillage d'éléments finis. Cela vaut également pour les réactions verticales.
Remarque au sujet de l'écoulement d'eau
Comme pour les forces de réaction dans l'analyse des contraintes, les flux ponctuels au niveau des nœuds ayant des pressions interstitielles données sont évalués pour 1 m de longueur d'arc ayant un diamètre valant x(r). En cas d'analyse de déformation plane, les valeurs correspondantes sont prises pour 1 m. Les flux globaux correspondants (flux entrant / sortant) peuvent être déterminés à partir des flux ponctuels [m3/jour/m] comme suit :
Calcul en déformation plane
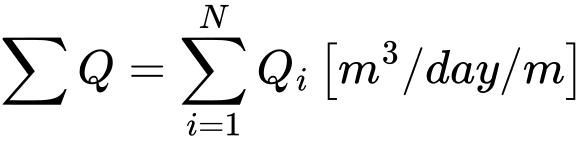
Calcul en condition axisymétrique
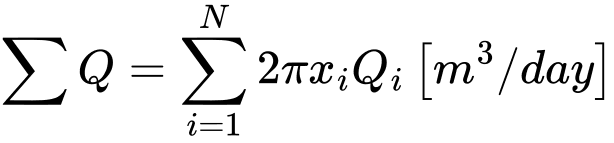
où N est le nombre de nœuds le long d'une ligne de maillage donnée, où les flux ponctuels Qi [m3/jour/m] sont calculés. Dans le cadre du calcul en condition axisymétrique, xi représente la coordonnée x d'un point donné. Par conséquent, le calcul en condition axisymétrique fournit la somme des flux entrant et sortant [m3/jour] à travers par exemple une surface cylindrique (ligne verticale) ou une surface circulaire (ligne horizontale).