Sarma法
Sarma法应列入极限状态的广义条分法范畴。各条块都必须满足静力平衡和力矩平衡条件。潜在滑动面上方的土体被切割面划分为若干条块,条块的两侧边界可以有不同的倾斜角度。各条块的受力情况如下图所示。
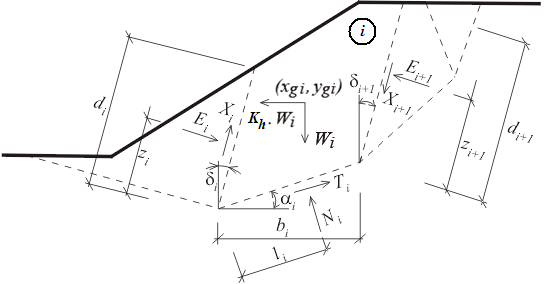 静力图 – Sarma法
静力图 – Sarma法
图中,Ei 、Xi 为条块间的法向力和剪切力。Ni、Ti 为滑面段上的法向力和剪切力。Wi 是条块重量,Kh*Wi 为Sarma法中达到极限状态时的水平力。在每个条块上都可以施加任意倾角的超载。分析时将定义的超载、因地面以上自由水位产生的超载和锚杆支护中的作用力一起考虑。将所有这些作用力分解到水平方向和竖直方向,然后分别计入到分量 Fxi 和 Fyi 中。
水平加速度系数 Kh 为一常量,将它引入到分析中是为了满足条块的平衡条件。计算安全系数时,Kh 与边坡的稳定性系数 SF 之间满足一定的关系。在一般的算例中,Kh 通常取零值。当 Kh 为非零值时,在软件中用来模拟水平超载,例如地震的作用(详细介绍参照下文)。
分析过程
极限平衡的计算
极限平衡的计算需要求解 6n-1 个未知量,其中 n 表示潜在滑动面上土体被划分的条块数,未知量为:
Ei | - | 条块间的法向力 |
Ni | - | 条块底面法向力 |
Ti | - | 条块底面剪切力 |
Xi | - | 条块间的剪切力 |
zi | - | Ei 的作用点位置 |
li | - | Ni 的作用点位置 |
Kh | - | 水平加速度系数 |
可列出 5n-1 个方程求解未知量:
a) 条块的水平作用力平衡方程:
![]()
b) 条块的竖向作用力平衡方程:
![]()
c) 条块的力矩平衡方程:
![]()
其中 rxi 和 ryi 为作用力 Fxi 和 Fyi 的力臂
d) 根据Mohr-Coulomb理论得到的法向力和剪切力的关系式:
![]()
![]()
其中: | P*Wi | - | 土条间接触面上的孔隙水压力合力值 |
| - | 土条间接触面上的内摩擦角平均值 | |
| - | 土条间接触面上的粘聚力平均值 |
很显然必须预先确定(预估)n-1 个变量值。如果预估作用力 Ei 的作用点,那么得到的结果误差相对较小。然后问题就变成静定受力的分析。求解方程组就能最终得到所有剩余未知变量的值。分析得到的主要结果是水平加速度系数 Kh。
计算边坡稳定性安全系数 SF
边坡稳定性安全系数 SF 以土的强度参数 c 和 tgφ 折减系数的形式引入分析中。在平衡分析中迭代使用被给定的边坡稳定性安全系数 SF 折减后的参数计算得到水平加速度系数 Kh,此迭代过程一直进行到系数 Kh 等于零或某指定值为止。
外荷载的影响
可以在边坡的表面施加任意梯形形状分布的倾斜荷载。输入实体超载的竖向分量(例如其重力)被计入到相应条块的重量中。这将改变条块的重量和其重心的位置。如果竖向分量的作用方向与重力方向相反,则将其纳入到作用力 Fyi 中。水平分量被添加到作用力 Fxi 中。
参考文献:
Sarma, S. K.: Stability analysis of embankments and slopes,Géotechnique 23, 423–433, 1973.