Calculation of charring layer
The depth of the charring layer dchar is the thickness of the material layer at the surface of the timber cross-section, that loses its ability to transfer stresses due to the degradation of mechanical properties. The material in this layer is charred, with no strength or even fallen off. The charring depth depends on charring rate, time, after which charring occurs (ie, the desired duration of fire resistance), and on a fire protection properties. Determination of the charring depth is the first important part of the fire resistance verification.
There are two basic values of the char depth used during the fire resistance verification. First value is the charring depth for one-dimensional charring dchar,0, depending on the design charring rate for one-dimensional charring β0. Second value is the notional charring depth dchar,n, which depends on the design notional charring rate under standard fire exposure βn. One-dimensional charring occurs when the flat wood element is exposed to fire from one side. If the cross-section is exposed to a fire from several sides, the increased carbonization in corners occurs. Since the calculation of the curvature in corners is complicated, the notional charring rate βn was defined. This notional charring rate performs increased values comparing to the one-dimensional charring rate β0, as the values are affected by the increased charring rate around the corners of the section.
Unprotected cross-section
The charring depth for unprotected cross-section is calculated using formula
![]()
Where is: | t |
|
β |
|
The values of charring rate β defined in EN 1995-1-2 corresponds to standard fire effects, that is described using standard temperature curve. For this type of fire, the charring rate β is a constant value without any time dependency. It corresponds to the fact that the temperature increases theoretically to infinity for the standard temperature curve over time.
Protected cross-section
The charring depth of protected cross-section doesn't rise linearly and doesn't begin immediately at time 0, as the beginning is shifted by a certain period tch. The charring course contains some marginal moments in which changes of charring rate occur. The first of them is the beginning of charring tch. Another important point is the time tf, that describes the time of protection failure. The values tch and tf may be identical for cases when the charring starts in time of protection failure. The charring rate of protected cross-section in time between tch and tf is slower comparing to the unprotected element. After the failure of fire protection the charring rate increases to a value, that is higher than the charring rate for unprotected element. Another important timestamp is the time ta, which is determined as the minimum of the two values: First value is the time, when the charring depth is identical to the charring depth of unprotected element with the same dimensions. The second value is the time when the charring depth is equal to 25mm. The charring rate β is the same as for unprotected cross-section after reaching this value. Following situations may occur for protected cross-sections:
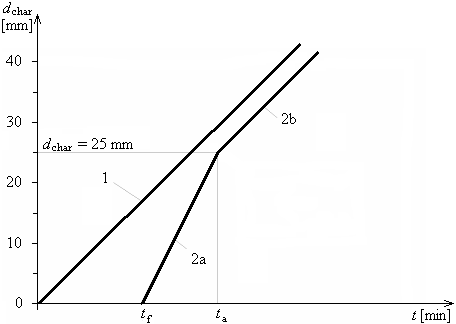 Development of charring depth in time for tf= tch, charring depth 25mm was reached earlier comparing to the unprotected cross-section
Development of charring depth in time for tf= tch, charring depth 25mm was reached earlier comparing to the unprotected cross-section
Where is: | 1 |
|
2 |
|
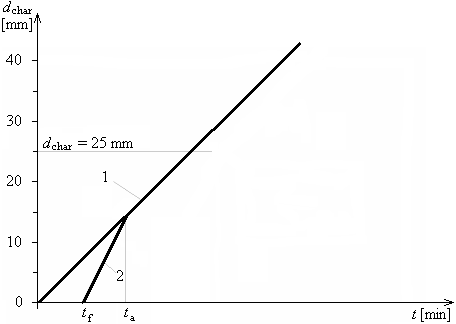 Development of charring depth in time for tf= tch, the charring depth equal to the charring depth of unprotected cross-section was reached earlier than the charring depth 25mm
Development of charring depth in time for tf= tch, the charring depth equal to the charring depth of unprotected cross-section was reached earlier than the charring depth 25mm
Where is: | 1 |
|
2 |
|
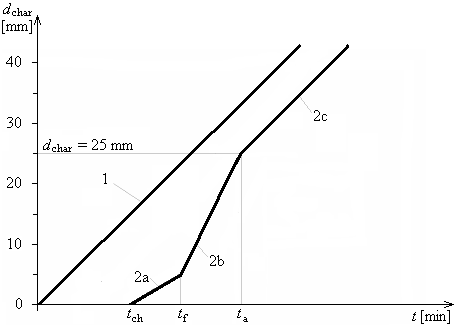 Development of charring depth in time for tf> tch, charring depth 25mm was reached earlier comparing to the unprotected cross-section
Development of charring depth in time for tf> tch, charring depth 25mm was reached earlier comparing to the unprotected cross-section
Where is: | 1 |
|
2 |
|
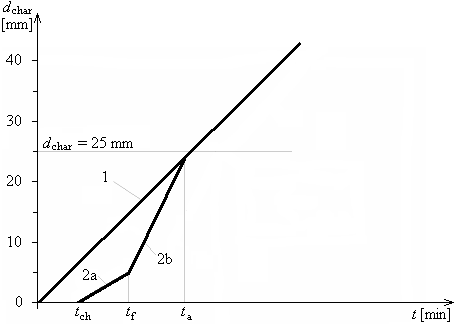 Development of charring depth in time for tf> tch, the charring depth equal to the charring depth of unprotected cross-section was reached earlier than the charring depth 25mm
Development of charring depth in time for tf> tch, the charring depth equal to the charring depth of unprotected cross-section was reached earlier than the charring depth 25mm
Where is: | 1 |
|
2 |
|
Time ta is calculated with the help of following procedures.
The increase of the charring depth for unprotected cross-section is calculated using this formula:
![]()
Where is: | t |
|
β |
|
Following formula is used for protected cross-sections with tf = tch for time between tf and ta:
![]()
Where is: | k3 |
|
Following formula is used for protected cross-sections with tf > tch for time between tf and ta:
![]()
Where is: | k3 |
|
df |
|
![]()
Where is: | k2 |
|