Únosnost v ohybu
Výpočtový moment únosnosti pro průřezy 1. a 2. třídy je dán vztahem
![]()
kde je: | Wpl,y, Wpl,z |
|
fy |
| |
γM0 |
|
Pro průřezy 3. a 4. třídy počítáme moment únosnosti ve čtyřech bodech na každém průřezu. Tyto body jsou umístěny v rozích průřezu. Výpočtový moment únosnosti pro průřezy 3. třídy je dán vztahem
![]()
kde je: | iWy, iWz |
|
fy |
| |
γM0 |
|
Výpočtový moment únosnosti pro průřezy 4. třídy počítáme ze vztahu
![]()
kde je: | iWeff,y, iWeff,z |
|
fy |
| |
γM0 |
|
Pokud je průřez oslaben, počítá se ještě mezní únosnost oslabeného průřezu v ohybu. Pro 1. a 2. třídu se počítá podle vztahu
![]()
kde je: | Wpl,y,osl,Wpl,z,osl |
|
fu |
| |
γM2 |
|
Pro 3. třídu podle vztahu
![]()
kde je: | iWy,osl, iWz,osl |
|
fu |
| |
γM2 |
|
A pro 4. třídu podle vztahu
![]()
kde je: | iWy,eff,osl, iWz,eff,osl |
|
fu |
| |
γM2 |
|
Při posouzení se pak počítá s menší z hodnot Mc,Rd,y a Mc,Rd,y,osl resp. Mc,Rd,z a Mc,Rd,z,osl.
U průřezů namáhaných "velkým smykem" (blíže popsáno v kapitole "Malý a velký smyk") se počítá ještě redukovaná únosnost v ohybu daná vztahem
![]()
kde je: | iWpl,y,red, iWpl,z,red |
|
fy |
| |
γM0 |
|
Redukovaný plastický průřezový modul je počítán jako plastický průřezový modul s redukovanou únosností na těch částech průřezu, které přenášejí "velký smyk". Redukce je provedena pomocí součinitelů ρz a ρy stanovených podle kapitoly "Malý a velký smyk". Při posouzení průřezu se počítá s menší z hodnot Mc,Rd,y a Mc,Rd,y,red resp. Mc,Rd,z a Mc,Rd,z,red.
Vliv klopení na únosnost
Únosnost v ohybu s vlivem klopení je dána vztahy
![]()
kde je: | χLT,y, χLT,z |
|
Mc,Rd,y, Mc,Rd,z |
|
Součinitele klopení χLT,y resp. χLT,z závisí na hodnotě pružného kritického momentu při ztrátě příčné a torzní stability Mcr, počítaného podle vztahů
![]()
kde μcr je bezrozměrný kritický moment daný vztahy
![]()
![]()
kde kwt je bezrozměrný parametr kroucení:
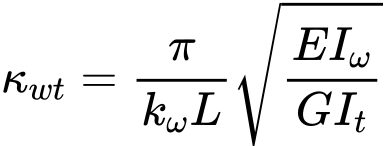
ζg je bezrozměrný parametr působiště zatížení vzhledem ke středu smyku:
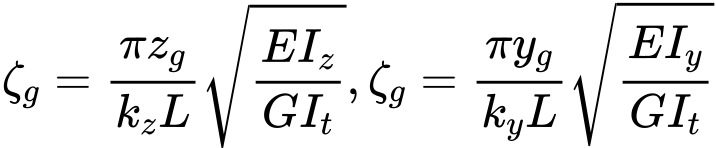
ζj je bezrozměrný parametr nesymetrie průřezu:
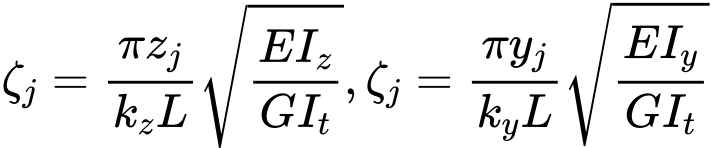
kde je: | C1, C2, C3 |
|
kz, ky, kw |
| |
E |
| |
G |
| |
Iz, Iy |
| |
L |
| |
Iω |
| |
It |
| |
zg, yg |
|
a zj a yj jsou dány vztahy
![]()
kde je: | zs, ys |
|
Na základě kritického momentu Mcr je stanovena poměrná štíhlost ![]() :
:
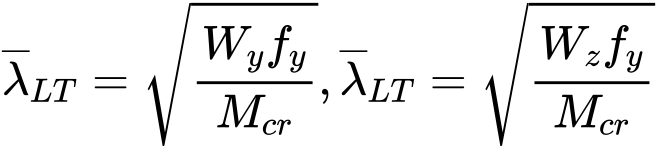
kde je: | Wy, Wz |
|
Podle tvaru posuzovaného průřezu je stanovena hodnota součinitele imperfekce při klopení αLT, která reprezentuje jednu z křivek klopení a, b, c, d. Součinitele vzpěrnosti χLT,y resp. χLT,z jsou pak počítány ze vztahů
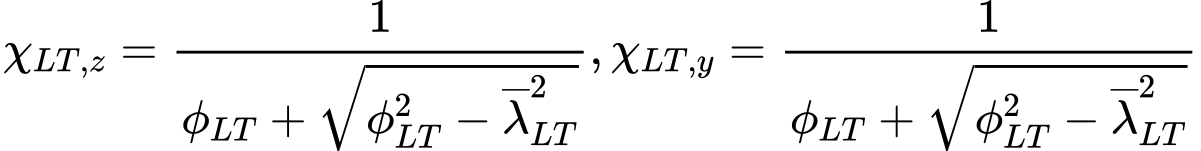
ale musí být splněno, že
![]()
kde
![]()
S vlivem klopení při ohybu momentem se nepočítá v případě, že je průřez tuhý v kroucení (jako například uzavřené průřezy) nebo působí-li ohybový moment v rovině menší únosnosti průřezu.