Modelo Mohr-Coulomb Modificado (MCM)
El modelo Mohr-Coulomb modificado representa una extensión del modelo original de Mohr-Coulomb. La superficie de fluencia se presenta, de forma similar a la superficie de fluencia por cizallamiento del modelo de suelo blando, o a la superficie de fluencia límite del modelo de suelo endurecido, mediante el criterio de falla de Matsuoka-Nakai. Una representación gráfica de la superficie de fluencia se desprende de la siguiente figura. De la proyección de la superficie de fluencia en los planos desviadores se desprende claramente que al disminuir el ángulo de fricción interna φ La superficie de rendimiento se aproxima al modelo de Drucker-Prager, mientras que para valores mayores del φ Se aproxima a la superficie de fluencia de Rankin. Además, la superficie de fluencia del modelo de Mohr-Coulomb modificado es una curva convexa suave y pasa por todos los vértices del modelo de Mohr-Coulomb. Por lo tanto, a diferencia del modelo de Drucker-Prager, la pendiente de la proyección en el plano meridiano Mφθ no es constante sino que depende del valor actual del ángulo Lode (Mφθ = Mφθ(φ, θ).
Por el contrario, la función de potencial plástico, que impulsa la evolución de las deformaciones plásticas, es idéntica a la del modelo de Drucker-Prager. Por lo tanto, es independiente del ángulo Lode. Sin embargo, depende del ángulo de dilatación ψ (Mψ = Mψ(ψ)). En general asumimos que φ ≠ ψ, que corresponde a la regla de flujo no asociado.
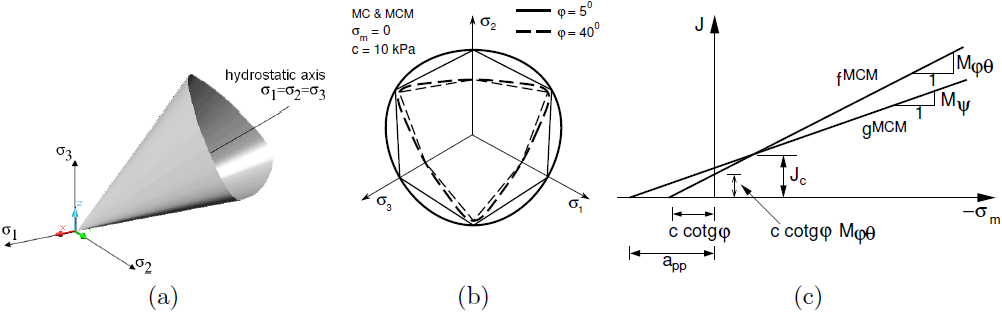 a) superficie de fluencia en el espacio de tensión principal, b) proyección en planos desviatorios y c) meridianos
a) superficie de fluencia en el espacio de tensión principal, b) proyección en planos desviatorios y c) meridianos
A diferencia de todos los demás modelos, independientemente de si son de plástico elástico perfecto o de plástico elástico con endurecimiento/ablandamiento, el modelo de Mohr-Coulomb modificado permite la evolución de la superficie de fluencia en función de la deformación plástica desviatoria equivalente Edpl. Más específicamente, definimos las funciones c(Edpl) y φ(Edpl). La variación lineal por tramos asumida de los parámetros de resistencia se hace evidente en la siguiente figura.
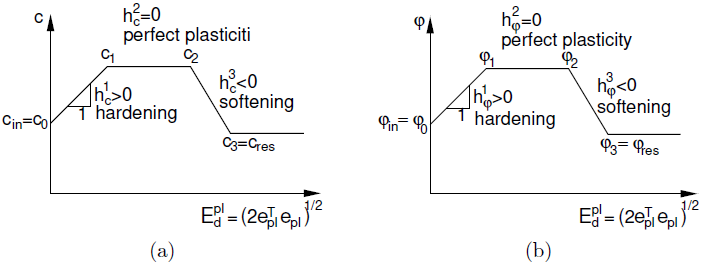 Evolución de los parámetros de resistencia al corte en función de la deformación plástica desviatoria equivalente: a) cohesión c b) ángulo de fricción interna φ
Evolución de los parámetros de resistencia al corte en función de la deformación plástica desviatoria equivalente: a) cohesión c b) ángulo de fricción interna φ
Al limitar la atención a pruebas de laboratorio simples (por ejemplo, compresión triaxial) y a la respuesta elástica-perfectamente plástica, el modelo proporciona predicciones idénticas a las generadas por el modelo Drucker-Prager o el modelo Mohr-Coulomb.
Lo mismo se aplica a la aplicación de condiciones drenadas o no drenadas. Para más información al respecto, consulte la presentación del modelo Drucker-Prager. Al ejecutar el análisis en condiciones no drenadas, aprovechando las características de endurecimiento/ablandamiento, se puede proceder sólo con el Tipo (1): análisis en tensión efectiva (cef, φe).
Al modelar el efecto de la dilatación (evolución de las deformaciones plásticas volumétricas positivas durante el cizallamiento plástico) El modelo de Mohr-Coulomb modificado permite considerar un valor constante del ángulo de dilatación ψ, de manera similar a los modelos Drucker-Prager, Mohr-Coulomb, Hoek-Brown, o para describir la evolución de ψ empleando la teoría de dilatación de Rowe de la siguiente manera:
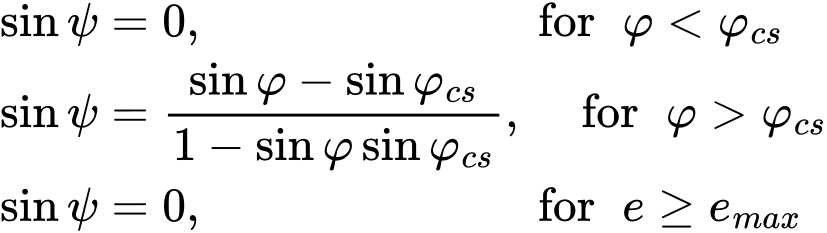
donde φ representa el valor actual del ángulo de fricción interna y φcs Es el ángulo de fricción del estado crítico. Claramente, la evolución de las deformaciones volumétricas positivas puede limitarse con la ayuda del ratio de vacíos máxima emax como se describe por ejemplo en el modelo Drucker-Prager.
Los parámetros del material que definen el modelo de Mohr-Coulomb Modificado se listan en la siguiente tabla. Los parámetros utilizados en el análisis en condiciones no drenadas, tipos 2 y 3, se pueden encontrar en la presentación del modelo de Drucker-Prager.
Símbolo | Unidades | Descripción | |
| [MPa] | Módulo de elasticidad | |
| [MPa] | Módulo de descarga/recarga | |
|
| Coeficiente de Poisson | |
| [kPa] | Coeficiente de cohesión efectivo | |
| [°] | Ángulo de fricción interna efectivo | |
| [°] | Ángulo de dilatación | |
| [kN/m3] | Peso a granel | |
|
| Ratio de vacíos inicial correspondiente al estado al final de la primera etapa de cálculo | |
|
| Ratio de vacíos máxima para terminar la dilatación (al limitar la dilatación) | |
| [°] | Ángulo de fricción del estado crítico (al determinar | |
| [1/K] | Coeficiente de expansión térmica (al considerar los efectos de la temperatura) | |
| - | gráfico que describe la evolución de c como una función de |
El modelo de Mohr-Coulomb modificado permite realizar el análisis de estabilidad. Se pueden realizar tanto el análisis estándar de estabilidad de taludes como el análisis de estabilidad dentro de una etapa de construcción determinada. La tarea se resuelve reduciendo gradualmente los parámetros de resistencia al corte máximo c, φ de la misma manera que se describe para el modelo Drucker-Prager. Durante el proceso de reducción, la función de endurecimiento/suavizado está desactivada.
Se espera que el modelo se mejore aún más con la introducción de la superficie de rendimiento de la capa de manera similar al modelo de Suelo blando.