Influence of Earthquake
Earthquake increases the effect of active pressure and reduces the effect of passive pressure. The theories used in our programs (Mononobe-Okabe, Arrango, JTJ 004-89, JTS 146-2012, SL 203-97, NCMA-SRW) are derived assuming cohesionless soils without influence of water. Therefore, all input soils are assumed cohesionless when employing these theories to address the earthquake effects. Earthquake effects due to surcharge are not considered in the program - the user may introduce these effects (depending on the type of surcharge) as "Applied forces".
The coefficient kh is assumed always positive and such that its effect is always unfavorable. The coefficient kv may receive both positive and negative value. If the equivalent acceleration av acts downwards (from the ground surface) the inertia forces kv Ws will be exerted on the soil wedge in the opposite direction (lifting the wedge up). The values of equivalent acceleration av (and thus also the coefficient kv) and inertia forces kv Ws are assumed as positive. It is clearly evident that the inertia forces act in the direction opposite to acceleration (if the acceleration is assumed upwards - av = - kv g then the inertia force presses the soil wedge downwards: - kv Ws. The direction with most unfavorable effects on a structure is assumed when examining the seismic effects.
For sheeting structures it is possible to neglect the effect of vertical equivalent acceleration kv Ws and input kv = 0.
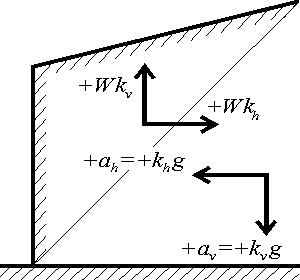 Sign convention
Sign convention
The seismic angle of inertia is determined from the coefficients kh and kv (i.e. angle between the resultant of inertia forces and the vertical line) using the formula:
![]()
where: | kv | - | seismic coefficient of vertical acceleration |
kh | - | seismic coefficient of horizontal acceleration |
Pressure from seismic effects
Increment of active earth pressure due to seismic effects (computed from the structure bottom) follows from:
![]()
![]()
where: | γi | - | unit weight of soil in the ith layer |
Kae,i | - | coefficient of active earth pressure (static and seismic) in the ith layer | |
Ka,i | - | magnitude of earth pressure in the ith layer due to Coulomb | |
hi | - | thickness of the ith layer | |
kv | - | seismic coefficient of vertical acceleration |
Reduction of passive pressure due to seismic load (computed from the structure bottom) is provided by:
![]()
![]()
where: | γi | - | unit weight of soil in the ith layer |
Kpe,i | - | coefficient of passive earth pressure (static and seismic) in the ith layer | |
Kp,i | - | magnitude of earth pressure in the ith layer due to Coulomb | |
hi | - | thickness of the ith layer | |
kv | - | seismic coefficient of vertical acceleration |
Active earth pressure coefficient Kae,i and passive earth pressure coefficient Kpe,i are computed using the Mononobe-Okabe theory or the Arrango theory. If there is groundwater in the soil body the program takes that into account.
The basic assumption in the program when computing earthquake is a flat ground surface behind the structure with inclination β. If that is not the case the program approximates the shape of terrain by a flat surface as evident from figure:
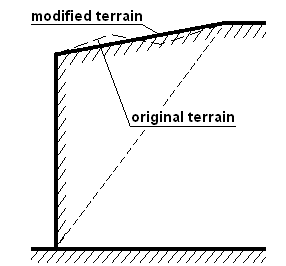 Terrain shape approximation
Terrain shape approximation
Point of application of resultant force
The resultant force is automatically positioned by the program into the center of the stress diagram. Various theories recommend, however, different locations of the resultant force - owing to that it is possible to select the point of application of the resultant force in the range of 0.33 - 0.7H (H is the structure height). Recommended (implicit) value is 0.66H. Having the resultant force the program determines the trapezoidal shape of stress keeping both the input point of application of the resultant force and its magnitude.