Online Help

Osová symetrie

Tento výpočetní modul je vhodný pro řešení rotačně souměrných úloh. Tomuto předpokladu musí vyhovovat jak geometrické uspořádání konstrukce, tak i zatížení. Vhodným příkladem je řešení svisle zatížené osamělé piloty, kruhového výkopu, nebo čerpání podzemní vody z kruhového vrtu.

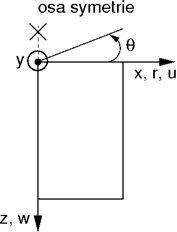Předpoklad osové souměrnosti

Podobně jako v případě úlohy rovinné deformace se jedná o obecně trojdimenzionální problém, který lze však opět převést na řešení rovinné úlohy (viz obr.). Řešení je pak vztaženo na 1 m délky oblouku o poloměru x(r). Osa symetrie vždy představuje počátek souřadnice x(r). Smykové složky deformace ve směru rotace lze zanedbat. Vedle složek napětí a deformace v rovině řezu uvažujeme také vznik obvodové normálové složky napětí a deformace. Příslušné nenulové složky napětí a deformace lze sestavit do vektoru napětí a deformace následovně:

Je zřejmé, že obvodová složka deformace a tudíž i dotčené normálové složky napětí nabývají na ose symetrie nekonečných hodnot. Z pohledu aproximace metodou konečných prvků vyžaduje jejich přesnější stanovení dostatečně jemnou síť v okolí osy symetrie.

Za pozornost stojí také aplikace liniového a plošného zatížení. Některé příklady zatížení povrchu terénu jsou prezentované na následujícím obrázku. Je zřejmé, že účinek těchto zatížení narůstá se vzdáleností od osy symetrie. Aplikace tohoto typu zatížení přímo na ose symetrie se tudíž ve výpočtu neprojeví. V tomto případě je nutno zvolit typ zatížení osy symetrie. Program umožňuje pouze silové bodové zatížení.

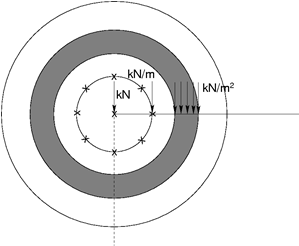Příklady přitížení terénu

V případě nosníkových prvků se jedná o řešení rovinné rotačně souměrné membrány s vlivem ohybových účinků. Nenulové stupně volnosti jsou shodné s příkladem deskového pásu uvažovaného při řešení úlohy rovinné deformace. Vedle osových (meridiálních) účinků je třeba uvažovat také membránové a ohybové účinky v obvodovém směru (viz následující obrázek).

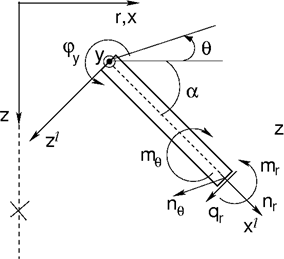Nosníkový prvek v osové symetrii

Příslušné složky vnitřních sil (viz obr.), vztažené na 1 m šířky lze sestavit do vektoru napětí následovně:

V případě kruhové desky nebo mezikruží (úhel α = 0) lze hovořit o radiálních a obvodových složkách vnitřních sil (viz následující obrázek).

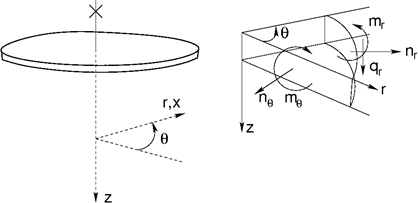Vnitřní síly na kruhové desce

Vztah mezi vnitřními silami a příslušnými složkami deformace lze obecně zapsat ve tvaru:

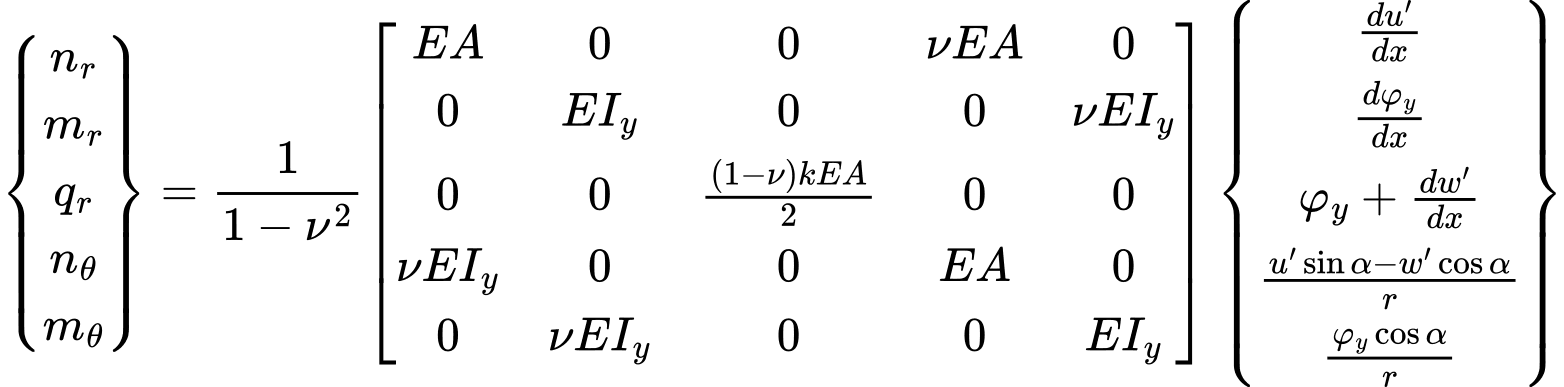
Položíme-li poloměr r roven nekonečnu, přejdeme k problému rovinné deformace. Za povšimnutí stojí, že v případě posouvajících sil je jejich hodnota, na rozdíl od problému rovinné deformace, silně odvislá od hustoty dělení nosníku na prvky. To platí i o svislých reakcích.

Poznámka k proudění

Připomeňme, že podobně jako reakce při analýze napětí jsou i hodnoty bodových toků v uzlech sítě s předepsanými pórovými tlaky vztaženy na 1 m délky oblouku o poloměru x(r). V případě rovinné deformace jsou příslušné hodnoty bodových toků vztaženy na 1 m délky. Tomu odpovídají i celkové hodnoty průtoků, které lze je určit z bodových toků [m³/den/m] následujícím způsobem:

Rovinná deformace

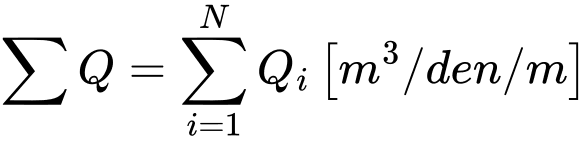
Osová symetrie

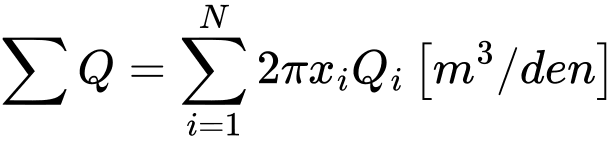
kde N je počet uzlů příslušné linie sítě, ve kterých jsou počítány bodové toky Q_i [m³/den/m]. V případě osové symetrie představuje x_i je hodnotu x-ové souřadnice daného bodu. Jedná se tedy o celkový průtok [m³/den] například válcovou plochou (svislá linie) nebo plochou kruhu (vodorovná linie).