Výpočet únosností
Při výpočtu únosností průřezu při požární situaci má rozhodující vliv změna deformačních a pevnostních vlastností oceli při vyšší teplotě. Tyto změny jsou vyjádřeny pomocí redukčních součinitelů ky,θ a kE,θ. ky,θ je součinitel redukce meze kluzu a kE,θ je součinitel redukce modulu pružnosti. Hodnoty obou těchto součinitelů jsou v normě EN 1993-1-2 tabelovány a leží v rozmezí od 1.0 při 20°C do 0.0 při 1200°C. Ve výpočtech pak vystupují redukované hodnoty meze kluzu a modulu pružnosti.
Výpočet smykové únosnosti
Smyková únosnost při požární situaci ve směru os z resp. y se počítají ze vztahu:
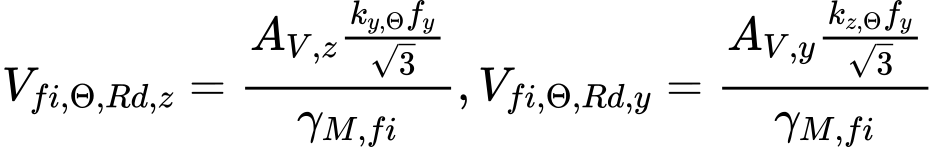
kde je: | AV,z, AV,y |
|
ky,θ |
| |
fy |
| |
γM,fi |
|
Pokud má průřez stěny podepřené na dvou okrajích rovnoběžně s osou z resp. y, započítává se do smykové únosnosti ve směru osy z resp. y ještě vliv boulení těchto stěn. Efekt boulení lze omezit zadáním příčných výztuh. Pro výpočet boulení stěny vlivem smyku je v programu použito tzv. jednoduché pokritické metody. Podle ní se smyková únosnost s vlivem boulení stanoví vztahem
![]()
kde je: | d |
|
tw |
| |
τba |
| |
γM,fi |
|
Výpočtová smyková únosnost ve směru osy zVfi,θ,Rd,z se určí jako menší z hodnot Vfi,θ,Rd,z a Vfi,θ,ba,Rd,z, únosnost ve směru osy y Vfi,θ,Rd,y se určí jako menší z hodnot Vfi,θ,Rd,y a Vfi,θ,ba,Rd,y. Pro stěny na jednom konci volné není boulení vlivem smyku řešeno.
Namáhání smykem od kroucení
U průřezů namáhaných kroucením se počítá se smykovými účinky od volného a od vázaného kroucení. Při namáhání krouticím momentem volného kroucení Tt se stanovuje smykové napětí τt. Pro otevřené průřezy je napětí τt dáno vztahem
![]()
kde je: | Tt |
|
It |
| |
t |
|
Pro uzavřené průřezy je napětí τt dáno vztahem
![]()
kde je: | Tt |
|
Ωt |
| |
t |
|
Při namáhání krouticím momentem vázaného kroucení Tω se smykové napětí τω počítá podle vztahu
![]()
kde je: | Tω |
|
Sω |
| |
Iω |
| |
t |
|
Smykové napětí se pak posuzuje podle vztahu
![]()
kde je: | ky,θ |
|
fy |
| |
γM,fi |
|
Při kombinaci namáhání smykovou silou a krouticím momentem se únosnosti ve smyku VRd,y a VRd,z redukují vzhledem k účinkům kroucení. Redukce se provádí podle vztahů
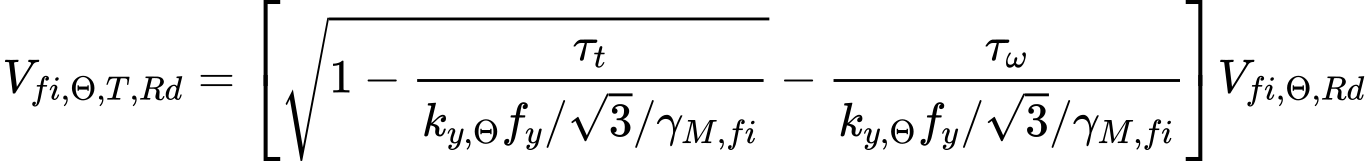
pro průřezy tvaru I a U a
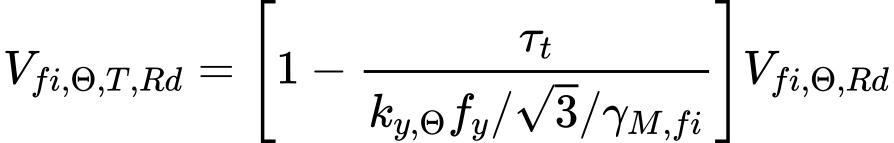
pro ostatní tvary průřezů.
Výpočet únosnosti v tahu
Únosnost průřezu při požární situaci v tlaku se počítá podle vztahu
![]()
kde je: | A |
|
ky,θ |
| |
fy |
| |
γM,fi |
|
Výpočet únosnosti v prostém tlaku
Únosnost průřezu při požární situaci v tlaku se počítá podle vztahu
![]()
kde je: | A |
|
ky,θ |
| |
fy |
| |
γM,fi |
|
Výpočet vzpěrné únosnosti
Vzpěrná únosnost průřezu při požární situaci je dána vztahem
![]()
kde je: | χfi |
|
A |
| |
ky,θ |
| |
fy |
| |
γM,fi |
|
Vzpěrná únosnost se počítá pro vybočení ve směrech os y a z nebo ve směrech hlavních os η a ζ. Součinitel vzpěrnosti χfi odpovídá poměrné štíhlosti ![]() a je dán vztahem
a je dán vztahem
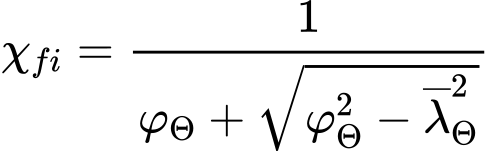
kde
![]()
kde
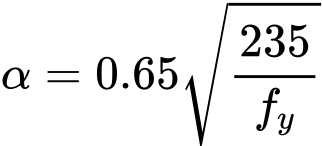
Poměrná štíhlost ![]() pro teplotu θ se určuje z výrazu
pro teplotu θ se určuje z výrazu
![]()
kde je: |
|
|
ky,θ |
| |
kE,θ |
|
Jako výpočtová vzpěrná únosnost průřezu Nb,fi,θ,Rd je vzata do posudku menší z únosností při vybočení k ose y nebo z.
Výpočet únosnosti v ohybu
Výpočtový moment únosnosti při požární situaci je dán vztahem
![]()
kde je: | W |
|
ky,θ |
| |
fy |
| |
γM,fi |
| |
κ1 |
| |
κ2 |
|
Pro průřezy 3. a 4. třídy počítáme moment únosnosti ve čtyřech bodech na každém průřezu. Tyto body jsou umístěny v rozích průřezu.
Vliv klopení na únosnost v ohybu
Únosnost v ohybu při požární situaci s vlivem klopení je dána vztahem
![]()
kde je: | χLT,fi |
|
Mc,fi,θ,Rd |
|
Součinitel klopení χLT,fi odpovídá poměrné štíhlosti ![]() a je dán vztahem
a je dán vztahem
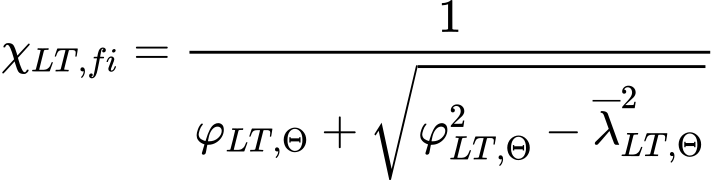
kde
![]()
kde
Poměrná štíhlost ![]() pro teplotu θ se určuje z výrazu
pro teplotu θ se určuje z výrazu
![]()
kde je: |
|
|
ky,θ |
| |
kE,θ |
|
Výpočet únosnosti pro namáhání bimomentem
Pro výpočet únosnosti průřezu na namáhání bimomentem při požární situaci uvažujeme pružné rozdělení napětí po průřezu, proto řešíme vždy jako průřez 3. nebo 4. třídy. Hodnoty únosnosti jsou stanoveny ve čtyřech rozích průřezu, kde očekáváme při namáhání bimomentem největší hodnoty napětí. Únosnost pro namáhání bimomentem při požární situaci je počítána podle vztahu
![]()
kde je: | Iω |
|
ω |
| |
ky,θ |
| |
fy |
| |
γM,fi |
| |
κ1 |
| |
κ2 |
|