Patní deska - únosnost patky
Při výpočtu únosnosti patky zatížené osovou silou a momentem se vychází z podmínky rovnováhy na patní desce. Při známé únosnosti tažené části patky Ft.Rd je možno určit polohu neutrální osy a momentovou únosnost MRd při působící normálové síle NEd za předpokladu plastického rozdělení vnitřních sil
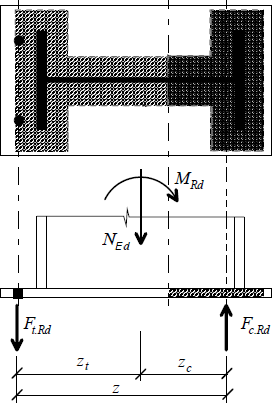 Rovnováha vnitřních sil na patní desce
Rovnováha vnitřních sil na patní desce
Počítáme-li pouze s účinnými oblasti pod pásnicemi sloupu (Steenhuis 1999) a působením NEd, MEd, řešení se zjednoduší, protože osa tlačené části a poloha tlakové reakce pod patní deskou splývá s osou pásnice. Předpoklad lze převzít i při kratším přesahu patní desky než je možná účinná šířka desky. Tahová síla působí v ose šroubů, při dvou řadách šroubů se počítá s výslednicí obou řad.
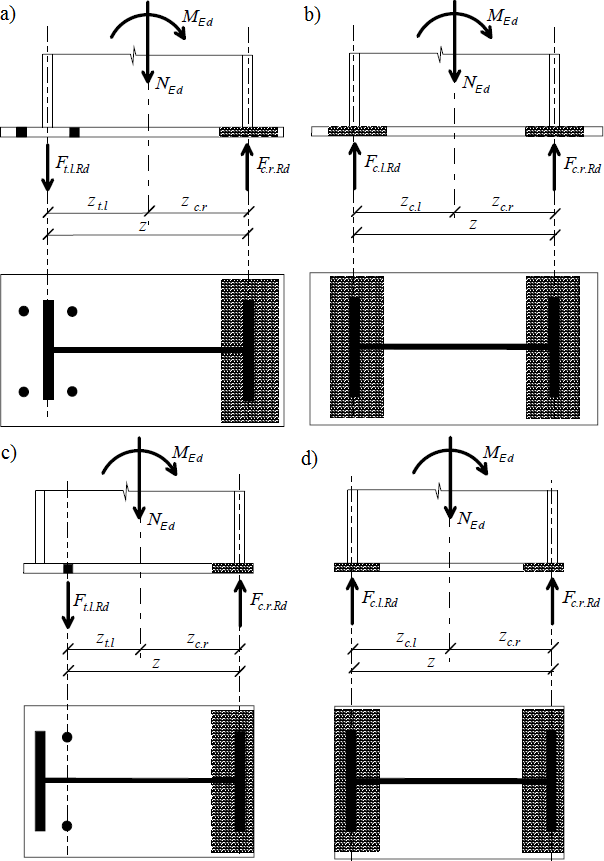 Rovnováha sil modelu s účinnou plochou pouze pod pásnicemi sloupu; a) dvě řady šroubů v tahu, b) obě pásnice v tlaku (velmi malý moment MEd), c) jedna řada šroubů v tahu a přesah patní desky menší než možná účinná šířka, d) obě pásnice v tlaku a přesah patní desky menší než možná účinná šířka
Rovnováha sil modelu s účinnou plochou pouze pod pásnicemi sloupu; a) dvě řady šroubů v tahu, b) obě pásnice v tlaku (velmi malý moment MEd), c) jedna řada šroubů v tahu a přesah patní desky menší než možná účinná šířka, d) obě pásnice v tlaku a přesah patní desky menší než možná účinná šířka
Síly představující únosnost tažené části Ft,l,Rd a tlačené části Fc,l,Rd, Fc,r,Rd byly určeny výše. Pokud vzniká tahová síla v kotevních šroubech, pro excentricitu zatížení platí e= MEd/NEd≥ zc.r a podle variant a) a c) lze vyjádřit namáhání tažené a tlačené části patky z momentové podmínky rovnováhy
![]()
![]()
Únosnost patky sloupu MRd při známé osové síle NEd lze stanovit jako menší z hodnot MEd vypočítaných podle vzorců výše.
![]()
Pokud je excentricita e= MEd /NEd < zc,r (obrázek výše, varianty b) a d)), nepůsobí ve šroubech tahová síla, ale pod oběmi pásnicemi vzniká tlaková reakce. Momentová únosnost je v tomto případě
![]()
Literatura
Steenhuis C. M.: Assembling procedure for base plates, report 98-NOC-R0447 TNO, Delft 1999, s. 79.